RESOLVER PROBLEMAS

DESCARGAR PROBLEMAS

COMPETENCIAS EN FRACCIONES

CLAVES PARA RESOLVER PROBLEMAS MATEMATICOS

GUÍA PRÁCTICA PARA SOLUCIONAR PROBLEMAS MATEMÁTICOS

September 02, 2015 Publicado por: Karen Johanna Bonilla Categoría: Matemáticas

Normalmente en los centros educativos el profesor enseña las matemáticas con ejercicios operacionales y luego, en la evaluación, pone problemas que parece que nunca enseñó; en realidad es necesario que aprendas a comprender mejor los problemas y que sepas la forma de solucionarlos.

Para tu tranquilidad te informamos que nos pasa a todos, así que no pienses que eres la única persona. Para ayudarte hemos decidido crear esta guía que te ayudará a solucionar problemas matemáticos de todas las ciencias que requieren cálculos o la aplicación de algún algoritmo.

INFOGRAFÍA: Top 5: Éxito en la resolución de problemas matemáticos

1. Para solucionar bien un problema matemático es necesario que lo leas en su totalidad ¡no te anticipes!,  ya que la lectura comprensiva te ayudará a recrear el problema en tu mente y así estarás listo para empezar. [Lee aquí nuestro artículo completo: Aprende cómo desarrollar la lectura crítica]

2. Muchos docentes les dicen a sus alumnos “imaginen qué es lo que esta pasando”, efectivamente imaginar el problema y, si es posible, dibujarlo te permitirá saber qué es lo que está sucediendo en realidad dentro de él.

3. Luego selecciona los datos y la pregunta. Escríbelos aparte para que tengas en cuenta qué te dan y qué te piden. Ten en cuenta las unidades, pues la mayoría de estudiantes las omiten y por esta razón no contestan lo que les preguntan; de esta manera dejarás atrás toda la información que no es valiosa para llegar a la solución del problema matemático.

4. Al tener los datos, busca la relación que hay entre ellos; para esto debes seguir las fórmulas, si es el caso, como en la física o la química, o emplear las palabras clave, que indican la operación correspondiente o que te permiten saber a qué se quiere referir el ejercicio, por ejemplo:

Al saber qué es lo que quiere el problema con la pregunta y la relación correcta de los datos, puedes realizar la o las operaciones matemáticas correspondientes para responder al problema; en esta parte asegúrate de que estás contestando realmente lo que te preguntan. En caso de que la respuesta no sea efectiva, devuélvete y realiza rápidamente todos los pasos anteriores para que verifiques qué hace falta o en dónde está el error. 

Ten presente que la práctica hace al maestro y no importa si al principio hay frustración con algún problema, sigue intentándolo, busca ejercicios similares,  busca otro camino para la solución… lo más importante es no rendirte.

RECONOCIMIENTO DE FRACCIONES

DESCARGAR VIDEO

LÓGICAS EN LAS MATEMATICAS

1. Nuevo: Encuentra la lógica en las siguientes operaciones y números.
   
   



2. SILENCIO. Si Ángela habla más bajo que Rosa y Celia habla más alto que Rosa, ¿habla Ángela más alto o más bajo que Celia?
   
3. LA NOTA MEDIA. La nota media conseguida en una clase de 20 alumnos ha sido de 6. Ocho alumnos han suspendido con un 3 y el resto superó el 5. ¿Cuál es la nota media de los alumnos aprobados?





4. LOS CUATRO ATLETAS. De cuatro corredores de atletismo se sabe que C ha llegado inmediatamente detrás de B, y D ha llegado en medio de A y C. ¿Podría Vd. calcular el orden de llegada?



5. SEIS AMIGOS DE VACACIONES. Seis amigos desean pasar sus vacaciones juntos y deciden, cada dos, utilizar diferentes medios de transporte; sabemos que Alejandro no utiliza el coche ya que éste acompaña a Benito que no va en avión. Andrés viaja en avión. Si Carlos no va acompañado de Darío ni hace uso del avión, podría Vd. decirnos en qué medio de transporte llega a su destino Tomás.



6. LOS CUATRO PERROS. Tenemos cuatro perros: un galgo, un dogo, un alano y un podenco. Éste último come más que el galgo; el alano come más que el galgo y menos que el dogo, pero éste come más que el podenco. ¿Cuál de los cuatro será más barato de mantener?.



7. TENIS DE CATEGORÍA. En un partido del prestigioso torneo de tenis de Roland Garros se enfrentaron Agasy y Becker. El triunfo correspondió al primero por 6-3 y 7-5. Comenzó sacando Agasy y no perdió nunca su saque. Becker perdió su servicio dos veces. Agasy rompió el servicio de su rival en el segundo juego del primer set y, ¿en qué juego del segundo set?



8. SERPIENTES MARINAS. Un capitán en el Caribe fue rodeado por un grupo de serpientes marinas, muchas de las cuales eran ciegas. Tres no veían con los ojos a estribor, 3 no veían nada a babor, 3 podían ver a estribor, 3 a babor, 3 podían ver tanto a estribor como a babor, en tanto que otras 3 tenían ambos ojos arruinados. ¿Cuál es el mínimo número de serpientes necesarias para que con ellas se den todas esas circunstancias?



9. EL PARO AUMENTA. Con motivo de realizar un estudio estadístico de los componentes de una población, un agente analizó determinadas muestra de familias. El resultado fue el siguiente:
   1) Había más padres que hijos.
   2) Cada chico tenía una hermana.
   3) Había más chicos que chicas.
   4) No había padres sin hijos.
   ¿Qué cree Vd. que le ocurrió al agente?



10. PARTIDO DE TENIS. Santana ganó a Orantes un set de tenis por 6-3. Cinco juegos los ganó el jugador que no servía. ¿Quién sirvió primero?



11. CABALLOS. El caballo de Mac es más oscuro que el de Smith, pero más rápido y más viejo que el de Jack, que es aún más lento que el de Willy, que es más joven que el de Mac, que es más viejo que el de Smith, que es más claro que el de Willy, aunque el de Jack es más lento y más oscuro que el de Smith. ¿Cuál es el más viejo, cuál el más lento y cuál el más claro?



12. EL EXPLORADOR CONDENADO. Un explorador cayó en manos de una tribu de indígenas, se le propuso la elección entre morir en la hoguera o envenenado. Para ello, el condenado debía pronunciar una frase tal que, si era cierta, moriría envenenado, y si era falsa, moriría en la hoguera. ¿Cómo escapó el condenado a su funesta suerte?
    
13. EL PRISIONERO Y LOS DOS GUARDIANES. Un sultán encierra a un prisionero en una celda con dos guardianes, uno que dice siempre la verdad y otro que siempre miente. La celda tiene dos puertas: la de la libertad y la de la esclavitud. La puerta que elija el prisionero para salir de la celda decidirá su suerte.
    El prisionero tiene derecho de hacer una pregunta y sólo una a uno de los guardianes. Por supuesto, el prisionero no sabe cuál es el que dice la verdad y cuál es el que miente.
    ¿Puede el prisionero obtener la libertad de forma segura?
    
14. EL PRISIONERO Y LOS TRES GUARDIANES. Imaginemos que hay tres puertas y tres guardias, dos en las condiciones anteriores y el tercero que dice verdad o mentira alternativamente. ¿Cuál es el menor número de preguntas que debe hacer para encontrar la libertad con toda seguridad?
    
15. LOS 3 PRESOS Y LAS BOINAS (1). El director de una prisión llama a tres de sus presos, les enseña tres boinas blancas y dos boinas negras, y les dice: «Voy a colocar a cada uno de ustedes una boina en la cabeza, el primero de ustedes que me indique el color de la suya será puesto en libertad».
    Si los presos están en fila, de manera que el primero no puede ver las boinas de los otros dos, el segundo ve la boina del primero y el tercero ve las boinas de los otros dos. ¿Por qué razonamiento uno de los presos obtiene la libertad?
    
16. LOS 3 PRESOS Y LAS BOINAS (2). El director de una prisión llama a tres de sus presos, les enseña tres boinas blancas y dos boinas negras, y les dice: «Voy a colocar a cada uno de ustedes una boina en la cabeza, el primero de ustedes que me indique el color de la suya será puesto en libertad».
    Si los presos pueden moverse, y por tanto ver las boinas de los otros dos. ¿Por qué razonamiento uno de los presos obtiene la libertad?
    
17. LOS MARIDOS ENGAÑADOS. Cuarenta cortesanos de la corte de un sultán eran engañados por sus mujeres, cosa que era claramente conocida por todos los demás personajes de la corte sin excepción. Únicamente cada marido ignoraba su propia situación.
    El sultán: «Por lo menos uno de vosotros tiene una mujer infiel. Quiero que el que sea la expulse una mañana de la ciudad, cuando esté seguro de la infidelidad».
    Al cabo de 40 días, por la mañana, los cuarenta cortesanos engañados expulsaron a sus mujeres de la ciudad. ¿Por qué?
     
18. EL PASTOR Un pastor tiene que pasar un lobo, una cabra y una lechuga a la otra orilla de un río, dispone de una barca en la que solo caben el y una de las otras tres cosas. Si el lobo se queda solo con la cabra se la come, si la cabra se queda sola con la lechuga se la come, ¿cómo debe hacerlo?.
    
19. EL CONDENADO A MUERTE. En los tiempos de la antigüedad la gracia o el castigo se dejaban frecuentemente al azar. Así, éste es el caso de un reo al que un sultán decidió que se salvase o muriese sacando al azar una papeleta de entre dos posibles: una con la sentencia "muerte", la otra con la palabra "vida", indicando gracia. Lo malo es que el Gran Visir, que deseaba que el acusado muriese, hizo que en las dos papeletas se escribiese la palabra "muerte". ¿Cómo se las arregló el reo, enterado de la trama del Gran Visir, para estar seguro de salvarse? Al reo no le estaba permitido hablar y descubrir así el enredo del Visir.
    
20. LAS DEPORTISTAS. Ana, Beatriz y Carmen. Una es tenista, otra gimnasta y otra nadadora. La gimnasta, la más baja de las tres, es soltera. Ana, que es suegra de Beatriz, es más alta que la tenista. ¿Qué deporte practica cada una?
    
21. SILOGISMOS. Ejemplo que está en todos los manuales de lógica elemental. El silogismo:
    
    «Los hombres son mortales,
    Sócrates es hombre.
    Luego, Sócrates es mortal».
    es indudablemente conocido e inevitablemente válido. Qué ocurre con el siguiente:
    
    «Los chinos son numerosos,
    Confucio es chino.
    Luego, Confucio es numeroso».
    
22. EL TORNEO DE AJEDREZ. En un torneo de ajedrez participaron 30 concursantes que fueron divididos, de acuerdo con su categoría, en dos grupos. En cada grupo los participantes jugaron una partida contra todos los demás. En total se jugaron 87 partidas más en el segundo grupo que en el primero. El ganador del primer grupo no perdió ninguna partida y totalizó 7'5 puntos. ¿En cuántas partidas hizo tablas el ganador?
    
23. LAS TRES CARTAS. Tres naipes, sacados de una baraja francesa, yacen boca arriba en una fila horizontal. A la derecha de un Rey hay una o dos Damas. A la izquierda de una Dama hay una o dos Damas. A la izquierda de un corazón hay una o dos picas. A la derecha de una pica hay una o dos picas. Dígase de qué tres cartas se trata.
    
24. TRES PAREJAS EN LA DISCOTECA. Tres parejas de jóvenes fueron a una discoteca. Una de las chicas vestía de rojo, otra de verde, y la tercera, de azul. Sus acompañantes vestían también de estos mismos colores. Ya estaban las parejas en la pista cuando el chico de rojo, pasando al bailar junto a la chica de verde, le habló así:
    Carlos: ¿Te has dado cuenta Ana? Ninguno de nosotros tiene pareja vestida de su mismo color.
    Con esta información, ¿se podrá deducir de qué color viste el compañero de baile de la chica de rojo?
    
25. BLANCO, RUBIO Y CASTAÑO. Tres personas, de apellidos Blanco, Rubio y Castaño, se conocen en una reunión. Poco después de hacerse las presentaciones, la dama hace notar:
    
    "Es muy curioso que nuestros apellidos sean Blanco Rubio y Castaño, y que nos hayamos reunido aquí tres personas con ese color de cabello"
    "Sí que lo es -dijo la persona que tenía el pelo rubio-, pero habrás observado que nadie tiene el color de pelo que corresponde a su apellido." "¡Es verdad!" -exclamó quien se apellidaba Blanco.
    Si la dama no tiene el pelo castaño, ¿de qué color es el cabello de Rubio?
    
26. LOS CIEN POLÍTICOS. Cierta convención reunía a cien políticos. Cada político era o bien deshonesto o bien honesto. Se dan los datos:
    a) Al menos uno de los políticos era honesto.
    b) Dado cualquier par de políticos, al menos uno de los dos era deshonesto. ¿Puede determinarse partiendo de estos dos datos cuántos políticos eran honestos y cuántos deshonestos?
    
27. COMIENDO EN EL RESTAURANTE. Armando, Basilio, Carlos y Dionisio fueron, con sus mujeres, a comer. En el restaurante, se sentaron en una mesa redonda, de forma que:
    - Ninguna mujer se sentaba al lado de su marido.
    - Enfrente de Basilio se sentaba Dionisio.
    - A la derecha de la mujer de Basilio se sentaba Carlos.
    - No había dos mujeres juntas.
    ¿Quién se sentaba entre Basilio y Armando?
    
28. SELLOS DE COLORES. Tres sujetos A, B y C eran lógicos perfectos. Cada uno podía deducir instantáneamente todas las conclusiones de cualquier conjunto de premisas. Cada uno era consciente, además, de que cada uno de los otros era un lógico perfecto. A los tres se les mostraron siete sellos: dos rojos, dos amarillos y tres verdes. A continuación, se les taparon los ojos y a cada uno le fue pegado un sello en la frente; los cuatro sellos restantes se guardaron en un cajón. Cuando se les destaparon los ojos se le preguntó a A:
    -¿Sabe un color que con seguridad usted no tenga?
    A, respondió: -No. A la misma pregunta respondió B: -No.
    ¿Es posible, a partir de esta información, deducir el color del sello de A, o del de B, o del de C?
    
29. LA LÓGICA DE EINSTEIN. Problema propuesto por Einstein y traducido a varios idiomas conservando su lógica. Einstein aseguraba que el 98% de la población mundial sería incapaz de resolverlo. Yo creo que Vd. es del 2% restante. Inténtelo y verá como tengo razón.
    Condiciones iniciales:
    - Tenemos cinco casas, cada una de un color.
    - Cada casa tiene un dueño de nacionalidad diferente.
    - Los 5 dueños beben una bebida diferente, fuman marca diferente y tienen mascota diferente.
    - Ningún dueño tiene la misma mascota, fuma la misma marca o bebe el mismo tipo de bebida que otro.
    Datos:
    1. El noruego vive en la primera casa, junto a la casa azul.
    2. El que vive en la casa del centro toma leche.
    3. El inglés vive en la casa roja.
    4. La mascota del Sueco es un perro.
    5. El Danés bebe té.
    6. La casa verde es la inmediata de la izquierda de la casa blanca.
    7. El de la casa verde toma café.
    8. El que fuma PallMall cría pájaros.
    9. El de la casa amarilla fuma Dunhill.
    10. El que fuma Blend vive junto al que tiene gatos.
    11. El que tiene caballos vive junto al que fuma Dunhill.
    12. El que fuma BlueMaster bebe cerveza.
    13. El alemán fuma Prince.
    14. El que fuma Blend tiene un vecino que bebe agua.
    ¿Quién tiene peces por mascota?
    
30. COLOCANDO NÚMEROS (1). Colocar un número en cada cuadro de una tabla de 3 filas x 3 columnas, teniendo en cuenta que:
     a) 3, 6, 8, están en la horizontal superior.
    b) 5, 7, 9, están en la horizontal inferior.
    c) 1, 2, 3, 6, 7, 9, no están en la vertical izquierda.
    d) 1, 3, 4, 5, 8, 9, no están en la vertical derecha.
31. COLOCANDO NÚMEROS (2). Colocar un número en cada cuadro de una tabla de 3 filas x 3 columnas, teniendo en cuenta que:
    
    a) 3, 5, 9, están en la horizontal superior.
    b) 2, 6, 7, están en la horizontal inferior.
    c) 1, 2, 3, 4, 5, 6, no están en la vertical izquierda.
    d) 1, 2, 5, 7, 8, 9, no están en la vertical derecha.
    
32. LA BARAJA ESPAÑOLA. En una mesa hay cuatro cartas en fila:
    1. El caballo esta a la derecha de los bastos.
    2. Las copas están mas lejos de las espadas que las espadas de los bastos.
    3. El rey esta mas cerca del as que el caballo del rey.
    4. Las espadas, mas cerca de las copas que los oros de las espadas.
    5. El as esta mas lejos del rey que el rey de la sota.
    ¿Cuáles son los cuatro naipes y en qué orden se encuentran?
    
33. COLOCANDO NÚMEROS (3). Colocar un número en cada cuadro de una tabla de 3 filas x 3 columnas, teniendo en cuenta que: 
    
    a) 4, 5, 6, están en la horizontal superior.
    b) 7, 8, están en la horizontal inferior.
    c) 2, 3, 4, 5, 8, 9, no están en la vertical izquierda.
    d) 1, 5, 6, 7, 8, 9, no están en la vertical derecha.
    
34. EN EL ASCENSOR. Cuatro jugadores de rugby entran en un ascensor que puede trasportar un máximo de 380 kilos. Para que no suene una alarma, que detendría al elevador por exceso de carga, tiene usted que calcular su peso total con gran rapidez. Pero, ¿cuanto pesa cada jugador? He aquí los datos: Pablo es quien pesa más: si cada uno de los otros pesara tanto como el, la alarma detendría el ascensor.
    Carlos es el mas ligero: ¡el ascensor podría subir a cinco como el¡ Renato pesa 14 kilos menos que Pablo, y solo seis menos que Jesús. Jesús pesa 17 kilos mas que Carlos. Los peces de Pablo y de Carlos son múltiplos de cinco.
    
35. COLOCANDO NÚMEROS (4). Colocar un número en cada cuadro de una tabla de 3 filas x 3 columnas, teniendo en cuenta que:
    
    a) 2, 5, 6, están en la horizontal superior.
    b) 4, 7, 8, están en la horizontal inferior.
    c) 2, 3, 4, 6, 7, 9, no están en la vertical izquierda.
    d) 1, 2, 4, 5, 8, 9, no están en la vertical derecha.
    
36. LA ORUGA Y EL LAGARTO. La oruga piensa que tanto ella como el lagarto están locos. Si lo que cree el cuerdo es siempre cierto y lo que cree el loco es siempre falso, ¿el lagarto está cuerdo? (Original de Lewis Carroll)
    
37. LOS TRES DADOS. Tengo tres dados con letras diferentes. Al tirar los dados puedo formar palabras como: OSA, ESA, ATE, CAE, SOL, GOL, REY, SUR, MIA, PIO, FIN, VID, pero no puedo formar palabras tales como DIA, VOY, RIN. ¿Cuáles son las letras de cada dado?
    
38. ¿SON MENTIROSOS? Andrés: Cuando yo digo la verdad, tú también.
    Pablo: Cuando yo miento, tu también.
    ¿Es posible que en esta ocasión uno mienta y el otro no?
    
39. PASTELES PARA NIÑOS. Un niño y medio se comen un pastel y medio en un minuto y medio. ¿Cuántos niños hacen falta para comer 60 pasteles en media hora?
    
40. LA BODA. Cuando María preguntó a Mario si quería casarse con ella, este contestó: "No estaría mintiendo si te dijera que no puedo no decirte que es imposible negarte que si creo que es verdadero que no deja de ser falso que no vayamos a casarnos". María se mareó. ¿Puede ayudarla diciéndola si Mario quiere o no quiere casarse?
    
41. EL ENCUENTRO. Ángel, Boris, César y Diego se sentaron a beber. El que se sentó a la izquierda de Boris, bebió agua. Ángel estaba frente al que bebía vino. Quien se sentaba a la derecha de Diego bebía anís. El del café y el del anís estaban frente a frente. ¿Cuál era la bebida de cada hombre?
    
42. EL NÚMERO. Buscamos un número de seis cifras con las siguientes condiciones.
    - Ninguna cifra es impar.
    - La primera es un tercio de la quinta y la mitad de la tercera.
    - La segunda es la menor de todas.
    - La última es la diferencia entre la cuarta y la quinta.
    
43. LA HILERA DE CASAS. En una hilera de cuatro casas, los Brown viven al lado de los Smith pero no al lado de los Bruce. Si los Bruce no viven al lado de los Jones, ¿quiénes son los vecinos inmediatos de los Jones?
    
44. COMPLETANDO. Completar la oración siguiente colocando palabras en los espacios: Ningún pobre es emperador, y algunos avaros son pobres: luego: algunos (.........) no son (.........).
    
45. EXAMEN DE HISTORIA. De las siguientes afirmaciones. ¿cuáles son las dos que. tomadas conjuntamente, prueban en forma concluyente que una o más niñas aprobaron el examen de historia?
    a) Algunas niñas son casi tan competentes en historia como los niños.
    b) Las niñas que hicieron el examen de historia eran más que los niños.
    c) Más de la mitad de los niños aprobaron el examen.
    d) Menos de la mitad de todos los alumnos fueron suspendidos.
    
46. CONDUCTORES Y SU SEXO. Las estadísticas indican que los conductores del sexo masculino sufren más accidentes de automóvil que las conductoras. La conclusión es que:
    a) Como siempre, los hombres, típicos machistas, se equivocan en lo que respecta a la pericia de la mujer conductora.
    b) Los hombres conducen mejor, pero lo hacen con más frecuencia.
    c) Los hombres y mujeres conducen igualmente bien, pero los hombres hacen más kilometraje.
    d) La mayoría de los camioneros son hombres.
    e) No hay suficientes datos para justificar una conclusión.
    
47. GASOLINA. Si al llegar a la esquina Jim dobla a la derecha o a la izquierda puede quedarse sin gasolina antes de encontrar una estación de servicio. Ha dejado una atrás, pero sabe que, si vuelve, se le acabará la gasolina antes de llegar. En la dirección que lleva no ve ningún surtidor. Por tanto:
    a) Puede que se quede sin gasolina.
    b) Se quedará sin gasolina.
    c) No debió seguir.
    d) Se ha perdido.
    e) Debería girar a la derecha.
    f) Debería girar a la izquierda.
    
48. NEUMÁTICOS. Todos los neumáticos son de goma. Todo lo de goma es flexible. Alguna goma es negra. Según esto, ¿cuál o cuáles de las siguientes afirmaciones son ciertas?
    a) Todos los neumáticos son flexibles y negros.
    b) Todos los neumáticos son negros.
    c) S¾lo algunos neumáticos son de goma.
    d) Todos los neumáticos son flexibles.
    e) Todos los neumáticos son flexibles y algunos negros.
    
49. OSTRAS. Todas las ostras son conchas y todos los conchas son azules; además algunas conchas son la morada de animalitos pequeños. Según los datos suministrados, ¿cuál de las siguientes afirmaciones es cierta?
    a) Todas las ostras son azules.
    b) Todas las moradas de animalitos pequeños son ostras.
    c) a) y b) no son ciertas.
    d) a) y b) son ciertas las dos.
    
50. PUEBLOS. A lo largo de una carretera hay cuatro pueblos seguidos: los Rojos viven al lado de los Verdes pero no de los Grises; los Azules no viven al lado de los Grises. ¿Quiénes son pues los vecinos de los Grises?
    
51. EL TEST. Tomás, Pedro, Jaime, Susana y Julia realizaron un test. Julia obtuvo mayor puntuación que Tomás, Jaime puntuó más bajo que Pedro pero más alto que Susana, y Pedro logró menos puntos que Tomás. ¿Quién obtuvo la puntuación más alta?
    
52. EL INTERRUPTOR. Un hombre esta al principio de un largo pasillo que tiene tres interruptores, al final hay una habitación con la puerta cerrada. Uno de estos tres interruptores enciende la luz de esa habitación, que esta inicialmente apagada.
    
    ¿Cómo lo hizo para conocer que interruptor enciende la luz recorriendo una sola vez el trayecto del pasillo?
    
    Pista: El hombre tiene una linterna.
53. El Padre de Ana tiene 4 hijas. Una se llama Ena, otra Ina y otra Ona. ¿Cómo se llama la otra hija?.
54. Hay meses que tiene 30 dias y otros 31 días. ¿Cuantos meses tienen 28 días?

PINTANDO APRENDO CON LAS FRACCIONES

PROBLEMAS MATEMATICO

Algunos consejos para resolver problemas

Hirió mi mente un relámpago,  que colmó mi deseo.

DANTE: Paradiso, Canto XXXIII

Por favor, dame un problema

Los matemáticos entendemos la palabra "problema" de forma diferente a la usual. Si le dices a un amigo "tengo un problema", seguro que ese amigo entiende que te sucede algo que puede tener consecuencias desagradables. Casi todo el mundo procura evitar los problemas y a nadie le gusta que le "calienten la cabeza" con problemas. A nadie... menos a los matemáticos. Para un matemático tener un buen problema es garantía de horas de trabajo interesante, a veces, incluso, apasionante. En todos los tiempos el deseo de resolver algunos grandes problemas ha sido el mayor estímulo para el progreso de las matemáticas. Hacer matemáticas consiste, esencialmente, en resolver y en proponer problemas. 

Te digo todo esto, porque ya es hora de que empieces a considerar los problemas como amigos que te brindan la oportunidad de progresar de una forma activa en tus estudios, de comprobar si de verdad sabes lo que crees saber y, a veces, de experimentar ese destello de plenitud gozosa que sobreviene cuando, después de horas de intenso trabajo, alcanzas la "iluminación" de la respuesta correcta, simple y elegante.  

¿Qué es un problema?

El verdadero problema es que hace ya mucho tiempo que en las enseñanzas medias se olvidaron de los problemas. No me preguntes por qué. Yo no soy ningún experto en el tema, pero mi impresión es que en algunas de las teorías pedagógicas de moda (las que hablan de enseñanza lúdica o de aprender a aprender y otras bobadas por el estilo) subyace una enorme desconfianza en la capacidad de los jóvenes para aprender. Por ello, no es extraño que en la Reforma de las enseñanzas medias los ejercicios más o menos triviales hayan acabado por sustituir a los bonitos problemas de antes, aquellos que proponían los profesores antes de que los teóricos de todas las reformas les convencieran de que sus alumnos eran demasiado torpes. Por eso, es muy posible que hayas llegado a la universidad sin haberte enfrentado nunca con un problema de verdad, un problema que no sea un mero ejercicio. Porque no son lo mismo.

EJERCICIOS

• De un vistazo sabes lo que te piden que hagas.
• Conoces de antemano un camino y no tienes más que aplicarlo para llegar a la solución.
• El objetivo principal es aplicar en una situación concreta, de forma más o menos mecánica, procedimientos y técnicas generales previamente ensayados.
• Proponen tareas perfectamente definidas.

PROBLEMAS

• Suele ser necesario leerlos con atención para entenderlos correctamente.  
• Sabes, más o menos, a dónde quieres llegar, pero ignoras el camino.
• El objetivo es que organices y relaciones tus conocimientos de forma novedosa. Suponen una actitud mental positiva, abierta y creativa.
• En general, son cuestiones más abiertas y menos definidas que los ejercicios.

ALGUNOS CONSEJOS QUE TE AYUDARÁN A PENSAR MEJOR

Para ser eficaz resolviendo problemas, es conveniente que tengas en cuenta las siguientes recomendaciones.

La actitud inicial es importante
Cuando nos enfrentamos a un problema es muy importante la actitud que tienes ante él. ¿Estás ansiosos por resolverlo o no tienes gana ninguna? ¿Tus condiciones físicas (cansancio, sueño, etc..) son las adecuadas? ¿Tienes curiosidad, disposición de aprender, gusto por el reto?

Ten confianza en tus capacidades
Con frecuencia, no es necesario saber mucho para resolver bien un problema. Basta con pensar correctamente. Actúa, pues, sin miedo, con tranquilidad, convencido de que está a tu alcance.

Sé paciente y constante
No abandones a la menor dificultad. Si te quedas atascado, no te des por vencido; piensa un nuevo enfoque del problema. Cada problema requiere su tiempo. 

Concéntrate en lo que haces
Resolver problemas es una actividad mental compleja. Requiere poner en tensión todos nuestros resortes mentales.

Busca el éxito a largo plazo
Aprender a resolver problemas es un proceso lento. Los frutos tardarán un cierto tiempo en llegar pero cuando notes los progresos sentirás una gran satisfacción.

 

ETAPAS EN LA RESOLUCIÓN DE UN PROBLEMA

No existen reglas que aseguren el éxito en la solución de problemas. Sin embargo, sí se pueden señalar algunos pasos generales para el proceso de resolverlos. Los que siguen están sacados del libro How To Solve It de George Polya y de los libros Aventuras Matemáticas y Para pensar mejor de Miguel de Guzmán cuya lectura te recomiendo vivamente. 

A Comprende el problema

Lee tranquilamente el enunciado. Puede ser necesario que lo leas varias veces, hasta estar seguro de haberlo entendido y de que no se te ha escapado ningún dato interesante. Has de tener muy claro en qué consiste, qué conoces, qué se te pide, cuáles son las condiciones... Esto es imprescindible para afrontar el problema con garantías de éxito. 

B Elabora un plan de actuación
Cuando ya estás seguro de haber entendido bien el problema y crees tener toda la información necesaria, es el momento de elegir una estrategia para resolverlo. Existe una gran variedad de estrategias que conviene que conozcas y que practiques para mejorar tu capacidad de resolver problemas. Al final te indico algunas de las más frecuentes.

C Lleva adelante tu plan

Ya tienes una estrategia que te parece adecuada. Trabájala con decisión y no la abandones a la primera dificultad. Pero si ves que las cosas se complican demasiado y que no te acercas nada a la solución, vuelve al paso anterior y prueba con una estrategia diferente. Por lo general hay varias formas de llegar a la solución y no podemos esperar acertar siempre con la más apropiada al primer intento. 

¿Salió? ¿Seguro? Revisa el resultado y cerciórate bien de que has llegado a la solución. Son innumerables las veces que creemos haber resuelto un problema y luego no es así. Las medias ideas y medias soluciones sirven de poco. 

D Mira atrás y reflexiona sobre todo el proceso
¿Has resuelto el problema? ¡Enhorabuena! ¿Has pasado un buen rato interesado, entretenido, intentándolo con ganas, y has acabado por no resolverlo? ¡Enhorabuena también! Se aprende mucho más de los problemas trabajados con interés y tesón... y no resueltos, que de los que se resuelven casi a primera vista. Ahora debes reflexionar sobre todo el proceso. Esta etapa puede ser la más provechosa de todas... y la que más a menudo olvidamos realizar. 

• Examina a fondo el camino que has seguido. ¿Cómo has llegado a la solución? ¿O, por qué no has llegado a la solución? ¿Ibas bien encaminado desde el principio? ¿Habías intuido la estrategia correcta en el paso B? ¿O, por qué no se te ocurrió pensar en ella? ¿Qué es lo que te engañó al escoger estrategias? ¿Cuál fue la chispa que te hizo intuir que iba a ir bien? 
• Revisa la solución desde un principio tratando de comprender bien no sólo que funciona sino por qué funciona. Mira a ver si se te ocurre hacerlo de modo más simple. 
• Familiarízate con el método de solución, a fin de utilizarlo en problemas futuros. Descartes dijo una vez: "Cada problema que resolví se convirtió en una regla que más adelante me sirvió para solucionar otros problemas." 
• Reflexiona un poco sobre tu propio proceso de pensamiento y saca consecuencias para el futuro. Con experiencias repetidas como ésta tal vez te puedas hacer un diagnóstico de tu propio estilo de conocimiento. Cada uno tiene el suyo peculiar. ¿Cómo es tu pensamiento? ¿Visual o analítico? ¿Dependes mucho de la expresión verbal o de la fórmula escrita? ¿Tiendes a pensar en círculos, obsesivamente? ¿Tiendes al compromiso con una sola idea, sin flexibilidad? ¿Cómo podrías fomentar la fluencia espontánea de ideas variadas, originales, novedosas? Si lo consigues, tendrás una gran ventaja al saber en qué clases de problemas te puedes ocupar con ventaja y en cuáles tu probabilidad de éxito no es tan grande. Sabrás cómo abordar problemas, no ya matemáticos, sino de toda clase, aproximándote a ellos tratando de sacar el mejor partido posible de las ventajas de tu propio estilo.

E Redactar el proceso de resolución

Esfuérzate por redactar de forma clara, ordenada, elegante, que pueda ser comprendida con facilidad por otra persona. Es frecuente que al hacerlo te des cuenta de que hay algún punto que no sabes explicar bien o alguna dificultad que tú habías pasado por alto. Aunque no hubieras llegado a resolverlo, hacer una buena redacción describiendo el proceso que has seguido, los sucesivos intentos, el porqué crees que no sale, etc., te ayudará a mejorar. Además, puede resultar muy útil para que quien te lo propuso pueda darte orientaciones que sean más adecuadas para ti.

ESTRATEGIAS PARA RESOLVER PROBLEMAS

• Buscar semejanzas con otros problemas
  Nada hay nuevo bajo el sol. ¿A qué te recuerda la situación? ¿No intuyes que tal vez sea como aquella otra?
  
• Reducir lo complicado a lo simple
  Normalmente el camino correcto para la resolución de un problema complicado es la división de este en otros más sencillos.
  
• Considerar casos particulares
  En algunas ocasiones, experimentar con casos particulares te pone en la pista correcta para resolver el caso general.
  
• Hacer un dibujo
  A veces, una imagen vale más que mil palabras. En el dibujo o esquema que hagas debes incorporar los datos realmente importantes y prescindir de lo demás. No necesitas hacer un dibujo muy preciso. El objetivo es que sirva de apoyo para avanzar en la resolución.
  
   
• Estudiar todos los casos posibles
  Se trata de ver todas y cada una de las posibilidades y analizar si se pueden aceptar o descartar y por qué.
  
• Elegir una buena notación
  Eligiendo una buena notación, un problema se puede simplificar notablemente. El objetivo es relacionar los datos con las variables elegidas y tratar de hacer los cálculos de la mejor manera posible. A la hora de elegir una buena notación, debemos tener presente que ésta sea clara, concisa y sin ambigüedades. La notación mejor es la que expresa abreviadamente la función misma de los elementos que representa.
  
   
• Incorporar algo adicional
  A veces, al incorporar un elemento nuevo, por ejemplo, una línea o una incógnita, se ponen de manifiesto relaciones que de otra forma pueden pasar desapercibidas.
  
• Ensayo y error
  Es una estrategia muy utilizada en nuestra vida: obramos de una determinada manera, observamos qué pasa, decidimos otras alternativas, etc. Estamos procediendo por ensayo y error. En matemáticas se suele emplear en multitud de ocasiones.
  
• Trabajar hacia atrás
  A veces es de gran ayuda imaginar que el problema está resuelto y trabajar paso a paso hacia atrás hasta llegar a la información conocida. Sólo entonces estarás en condiciones de recorrer en sentido contrario el camino y construir una solución.
  
• Razonamiento indirecto
  Ocasionalmente será apropiado atacar el problema de manera indirecta.  Supongamos que no... ¿a dónde nos lleva? Esto es el argumento que se llama indirecto o por reducción al absurdo. Para demostrar que P implica Q se puede suponer que P es verdadera y Q es falsa, y tratar de ver por qué esto es imposible.
  
• Aprovechar la simetría
  En algunos problemas existen, a veces encubiertas, ciertas regularidades o simetrías que pueden aprovecharse para resolverlos.
  
• Usar técnicas generales
  Por ejemplo, para demostrar resultados que involucran un entero positivo n, es de utilidad valerse del Principio de Inducción matemática. Otras veces, puede ser útil el llamado principio del palomar que se expresa así: si tienes n objetos que repartir en menos de n cajas, entonces en alguna de las cajas tienes que poner al menos dos objetos.
  
• Usar programas de cálculo simbólico
  Si puedes hacerlo ¿por qué no? Programas como Mathematica, Maple o Derive pueden proporcionarte una gran ayuda en muchas situaciones pues permiten hacer un tratamiento gráfico o numérico preciso. 

FRACCIONARIOS

Números fraccionarios. Se encuentran dentro del conjunto de los números racionales (Q) y se expresan de las forma a/b o como una expresión decimal periódica.
Surgen por la necesidad de dar solución a la división en el conjunto de los números naturales.

Contenido

 [ocultar] 

• 1 Introducción
  • 1.1 Definición
  • 1.2 Formas de expresión
• 2 Representación de los números fraccionarios sobre una recta numérica
• 3 Ordenar y comparar números fraccionarios expresados en diferentes formas
• 4 Adición y sustracción de números fraccionarios
• 5 Multiplicación y división de números fraccionarios
  • 5.1 Multiplicación
  • 5.2 División
  • 5.3 Vease
• 6 Fuente

Introducción

Los números están en cada una de las acciones de la vida cotidiana y con ellos podemos contar, ordenar, medir y comparar dos o varias cantidades.
Para cada acción siempre se utilizan diferentes tipos de números.
Un mismo número puede representar cantidades diferentes de acuerdo con su significado, y en otras ocasiones, números expresados de formas diferentes pueden tener el mismo significado.

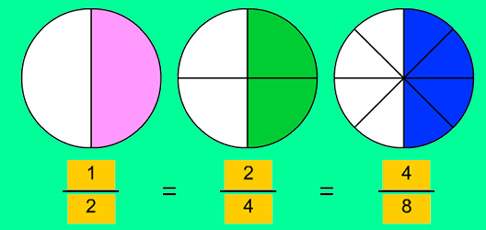
Diferentes números expresando la misma cantidad.

A partir de las diferentes operaciones de cálculo que podemos realizar con los números, han ido surgiendo los conjuntos numéricos y dentro de ellos los el de los números fraccionarios.

Definición

Los números fraccionarios o fracciones comunes se forman al plantear una división entre dos números naturales, teniendo en cuenta que siempre el divisor debe ser diferente de cero.

En un número fraccionario o fracción, el denominador indica las partes en que se divide la unidad y el numerador indica las partes que se toman.

Formas de expresión

Una fracción puede considerarse como el cociente exacto de dividir el numerador entre el denominador, de ahí que se pueda escribir también como el cociente a : b. 
Una fracción representa un número natural cuando al dividir el numerador por el denominador el resto de la división es cero.

Las fracciones comunes se pueden expresar en notación decimal. El número que se encuentra a la izquierda de la coma es la parte entera y las cifras que quedan situadas a la derecha de la coma son la parte decimal. La primera cifra después de la coma representa las décimas, la segunda las centésimas, la tercera las milésimas y así sucesivamente.

10 décimas forman una unidad, 10 centésimas forman una décima y 10 milésimas forman una centésima. Luego una unidad tiene 10 centésimas, 100 centésimas y 1000 milésimas. 

También existen las fracciones propias y las impropias:

• Una fracción se llama propia si su numerador es menor que su denominador.
• Una fracción se llama impropia si su numerador es mayor que su denominador. Se puede expresar como un número mixto formado por un número natural más una fracción propia.
• Si el numerador de una fracción es múltiplo del denominador, la fracción representa un número natural.

Representación de los números fraccionarios sobre una recta numérica

Las fracciones propias o expresiones decimales cuya parte entera es cero, siempre estarán situadas entre 0 y 1. Para representarlas se divide la unidad en tantas partes iguales como indique el denominador y posteriormente se determina el punto que representa las partes que indica el numerador. Si la fracción es un medio, la unidad se divide en dos partes iguales y el punto que corresponde a esa fracción es el que indica la mitad de la unidad. Para representar en la recta numérica una expresión decimal se puede expresar como fracción común (aunque no es necesario).

En muchas ocasiones se ubica por su significado. Las fracciones impropias, que pueden aparecer representadas como números mixtos o expresiones decimales donde la parte entera es diferente de cero, siempre se ubican en la recta numérica a la derecha de 1. Para ello se ubica primero el punto correspondiente a la parte entera y a partir de él, se determina en qué punto de la próxima unidad está ubicada la fracción o parte decimal del número, siendo este último, el lugar de la recta numérica donde queda situado este número fraccionario o fracción.

El menor número fraccionario es cero pero entre un número fraccionario y otro existen infinitos números más, luego no tienen antecesor ni sucesor. Se dice que este dominio numérico es un dominio denso.

Ordenar y comparar números fraccionarios expresados en diferentes formas

Al igual que en los números naturales, de dos fracciones es menor la que se encuentre situada más a la izquierda en la recta numérica. 
Existen varias maneras de comparar números fraccionarios (o fracciones comunes). 
De dos fracciones que tienen igual numerador es menor la que tenga mayor denominador. 
Las fracciones de igual denominador mantienen la misma relación de orden que sus numeradores. 
Cuando dos fracciones tienen diferentes numeradores y denominadores para su comparación se debe conocer que:

• Toda fracción propia es menor que 1 y que cualquier fracción impropia.
• Si las dos son propias o las dos son impropias se aplica el procedimiento del producto cruzado.

Adición y sustracción de números fraccionarios

En caso de las expresiones decimales la adición y la sustracción se calculan como si fueran números naturales, escribiendo la coma debajo de la coma de modo que las unidades del mismo orden queden una debajo de la otra. 
Para facilitar el cálculo en una sustracción donde el minuendo tenga menos cifras decimales que el sustraendo, se añaden al primero tantos ceros hasta igualar la cantidad de cifras decimales de ambos elementos y en el resultado se escribe la coma en el mismo lugar que ocupa en los elementos de la adición o sustracción. 
Para adicionar fracciones de igual denominador, se adicionan los numeradores y se mantiene el mismo denominador.

Para sustraer fracciones de igual denominador, al numerador del minuendo se le sustrae el numerador del sustraendo y se mantiene el mismo denominador. 
En ambas operaciones el resultado se simplifica si es posible. 
Para adicionar o sustraer fracciones de diferente denominador se calcula el mínimo común múltiplo (m.c.m) de los denominadores, se amplían los numeradores y luego se adicionan o se sustraen, manteniendo en el resultado el denominador. El resultado se simplifica si es posible. 
La adición de números naturales y fraccionarios es conmutativa y asociativa. 
El conocimiento de estas propiedades nos permite aplicarlas para realizar cálculos de una forma más ventajosa. 
La sustracción de números naturales y fraccionarios por su parte, no es conmutativa ni asociativa.

Multiplicación y división de números fraccionarios

Multiplicación

Para multiplicar expresiones decimales donde se calcula el producto como si los factores fueran números naturales y en el resultado se ubica la coma decimal contando a partir de la derecha tantos lugares decimales como haya en los dos factores juntos.
En el caso de que los factores sean fracciones, se simplifica si es posible y luego se multiplica numerador con numerador y denominador con denominador. También puede multiplicarse primero y después simplificar el resultado. 
La multiplicación de números naturales y fraccionarios es conmutativa y asociativa, y al igual que en la adición, la aplicación de estas propiedades puede resultar ventajosa para el cálculo. 
Para dividir un número natural entre una expresión decimal (123 : 0,6) o una expresión decimal entre otra (1,02 : 0,5) se procede a transformar la divisiónpara eliminar la coma del divisor. Para lograrlo se multiplica el dividendo y el divisor por 10, 100, 1000,… según la cantidad de lugares decimales que tenga divisor y se procede a hacer la división. 
Otra forma sería multiplicar dividendo y divisor por 10, 100, 1000,… atendiendo a la cantidad de lugares decimales del que mayor cantidad de estas cifras tenga. Luego se dividen los números naturales que se obtienen. 
Al terminar de dividir todos los dígitos que tiene el dividendo, si la división no resulta exacta, se coloca la coma decimal en el cociente para poder continuar la división.

División

En el caso de la división de fracciones se procede de la siguiente forma:

• La división se expresa como la multiplicación del dividendo por el recíproco del divisor.
• Se resuelve la multiplicación indicada.

En el caso de que alguna de las fracciones originales tenga simplificación podemos realizarla antes de realizar el primer paso.

CUENTO EL NUMERO CERO

DESCARGAR CUENTO

FORMULARIO NÚMEROS NATURALES

DESCARGA FORMULARIO 2

FORMULARIO DE OPERACIONES BASICAS

DESCARGAR FORMULARIO

GUIAS POSTPRIMARIA DE MATEMATICAS

DESCARGAR GUIAS

IMPORTANCIA DE LOS CUADROS MAGICOS

Importancia de jugar cuadrados mágicos

Jugar a crear y resolver cuadrados mágicos, favorece la realización de cálculos mentales, la comprensión de conceptos matemáticos como la adición, promueve el ingenio, la creatividad y la imaginación, permite ver las matemáticas más divertidas, facilita la adquisición de un sentido de autodominio y el desarrollo tanto del pensamiento lógico, como  de la autoestima en las niñas, los niños y los adolescentes, ; según afirman varios educadores, psicólogos e investigadores sociales de los juegos lógicos matemáticos.

Se puede dibujar un cuadrado y dividirlo en 9, 16, 25 cuadrados, o más. Estos cuadraditos se llaman celdas o casillas, en cada una de las cuales se debe ubicar un número entero, de forma que la suma de las filas, de las columnas y de las dos diagonales principales da siempre el mismo resultado, y el número que resulta se conoce como constante mágica. Ningún número de las casillas puede repetirse.

En este ejemplo, se puede ver que los números distribuidos van del 1 al 9.  Ahora determina la constante mágica.

El número de filas determina el denominado “orden” o “módulo del cuadrado”, así, los de tres filas y tres columnas, como el del ejemplo, se conocen como cuadrados de orden tres, los hay también, de orden cuatro y cinco, entre otros.  No hay cuadrados de orden dos.

Los cuadrados  mágicos eran conocidos por los matemáticos chinos que vivieron 45 siglos antes de Mahoma, el fundador de la religión islámica.  A su origen está ligado el de los sudokus y, en la antigüedad fueron usados como amuletos, para prevenir enfermedades e incluso para predecir el futuro.  A través de la historia han merecido la atención de diferentes matemáticos y científicos, entre los que se destaca Benjamín Franklin (1706 – 1790), reconocido político, científico e inventor estadounidense.

COMO CONSTRUIR UN CUADRO MAGICO

CUADRADOS  MÁGICOS

       Los cuadrados mágicos son ordenaciones de números en celdas formando un cuadrado, de tal modo que la suma de cada una de sus filas, de cada una de sus columnas y de cada una de sus diagonales dé el mismo resultado.

       Si la condición no se cumple para las diagonales, entonces se llaman cuadrados latinos.

       El origen de los cuadrados mágicos es muy antiguo. Los chinos y los indios los conocían antes del comienzo de la era cristiana.

       Los cuadrados mágicos se clasifican de acuerdo con el número de celdas que tiene cada fila o columna. Así, uno con 5 celdas se dice que es de quinto orden. No existen cuadrados mágicos de orden 2.

       Aunque todos los matemáticos han reconocido siempre la falta de aplicaciones de los cuadrados mágicos, algunos se han ocupado de ellos con mucha atención: el mérito y gracia del juego está en su insospechada dificultad.

       Si a, b y c son tres números enteros cualesquiera, la siguiente disposición muestra la forma general de un cuadrado mágico de orden 3:
  

a+b	a-(b+c)	a+c
a-(b-c)	a	a+(b-c)
a-c	a+(b+c)	a-b

       No hay métodos generales para construir cuadrados mágicos, sobre todo para los de orden par. Veamos un modo de construir fácilmente cuadrados mágicos de orden impar.

       1.    Tomemos una serie aritmética cualquiera, para mayor comodidad la serie de los números naturales, y coloquemos el número 1 en la celda central de la fila superior.
       2.    La cifra consecutiva a una cualquiera debe colocarse en la celda que le sigue diagonalmente hacia arriba y hacia la derecha.
       3.    Si al hacer esto se sale del cuadrado por el límite superior del contorno del mismo, saltaremos a la celda de la columna siguiente hacia la derecha y en su fila inferior, si se sale por la derecha, se sigue por la primera celda, a partir de la izquierda, de la fila superior.
       4.    Cuando la celda siguiente está ocupada, el número consecutivo de la serie se coloca en la celda inmediatamente inferior a la del número precedente, comenzando así un nuevo camino en la dirección de la diagonal.

       Como ejemplo, realicemos un cuadrado mágico de quinto orden:
  

17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9

       Finalmente, puesto que las sumas siguen siendo iguales entre si cuando multiplicamos todos los números de las casillas por un mismo factor, o les añadimos un mismo sumando, es claro que podemos alterar fácilmente, en esta forma el llenado de las casillas.

 1.   SUMA 15. Construye un cuadrado mágico de 3x3. (Suma=15)

 2.   SUMA 24. Coloca nueve números consecutivos en un cuadrado de 3x3, de manera que la suma de las filas y la de las columnas sea 24.

 3.   SUMA 18. Construye el cuadrado mágico de 3x3 tal que la suma de los 3 numeros elegidos sea 18.

 4.   OTRA SUMA DE 18. Coloca tres números consecutivos en un cuadrado de 3x3, de manera que la suma de las filas y la suma de las columnas sea 18.

 5.   DEL 10 AL 18. Halla el número K, sabiendo que el cuadrado en el cual está inscrito es mágico y se compone de los números de 10 a 18.

	K

 6.   A COMPLETAR. Completa el siguiente cuadrado para que sea mágico.

67		43
	73

 7.   SUMA 34. Construye un cuadrado mágico de 4x4. (Suma=34)

 8.    COMPLETA 3x3. Completa los casilleros que faltan para que resulte mágicos el siguiente cuadrado:

7		5
	8
11		9

 9.    COMPLETA 5x5. Completa los casilleros que faltan para que resulte mágicos el siguiente cuadrado:

11		7		3
	12		8
17		13		9
	18		14
23		19		15

10.    CALCULA: A, B, C, D , E. Halla A, B, C, D, E en el siguiente cuadrado mágico:

15	A	35
50	B	C
25	D	E

11.   CUADRADO DIABÓLICO. Construye un cuadrado mágico de 4x4 (Suma=34). Los elementos de cada una de las nueve matrices 2x2 que componen el cuadrado también deben sumar 34.

12.    ORIGINAL 4X4. ¿Por qué es muy original el siguiente cuadrado mágico?

96	11	89	68
88	69	91	16
61	86	18	99
19	98	66	81

13    RELLENA 5x5. Completa los casilleros que faltan para que resulte mágico el siguiente cuadrado:

1	20		23
24		2		10
17		25	14
15	4		7	21
	22	11		19

14.    CON LOS PARES. Construye un cuadrado mágico con los 9 primeros números pares de modo que las filas, columnas y diagonales sumen 30.

15.    CON LOS IMPARES. Construye un cuadrado mágico con los 9 primeros números impares de modo que las filas, columnas y diagonales sumen 27.

16.    PROBLEMA REVERSIBLE. a) Coloque en cada cuadrado libre un número menor que 10, de tal manera que en cada fila y en cada columna haya un número que se repita exactamente dos veces, y que la suma (de cada fila y de cada columna), sea 17.
         b) Dé la vuelta al cuadrado y resuélvalo nuevamente.
  

			8
	6
		6